Eigenvalues and Eigenvectors

2013. 1. 24. 01:09

The scalar λ is eigenvalue of a square matrix A, and x is eigenvector of A.

Eigenvector

Matrix A acts by stretching the vector x, not changing its direction, so x is an Eigenvector of A.

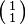The transformation matrix $\bigl[ \begin{smallmatrix} 2 & 1\\ 1 & 2 \end{smallmatrix} \bigr]$ preserves the direction of vectors parallel to $\bigl( \begin{smallmatrix} 1 \\ 1 \end{smallmatrix} \bigr)$ (in blue) and $\bigl( \begin{smallmatrix} 1 \\ -1 \end{smallmatrix} \bigr)$ (in violet). The points that lie on the line through the origin, parallel to an eigenvector, remain on the line after the transformation. The vectors in red are not eigenvectors, therefore their direction is altered by the transformation.

Dominant Eigenvalue and Dominant Eigenvector

Eigenvalues of a graph

In spectral graph theory, an eigenvalue of a graph is defined as an eigenvalue of the graph's adjacency matrix A, or (increasingly) of the graph's Laplacian matrix (see alsoDiscrete Laplace operator), which is either T−A (sometimes called the Combinatorial Laplacian) or I−T^−1/2AT^−1/2 (sometimes called the Normalized Laplacian), where T is a diagonal matrix with T_v,v equal to the degree of vertex v, and in T^−1/2, the v^th diagonal entry is deg(v)^−1/2. The k^th principal eigenvector of a graph is defined as either the eigenvector corresponding to the k^th largest or k^th smallest eigenvalue of the Laplacian. The first principal eigenvector of the graph is also referred to merely as the principal eigenvector.

The principal eigenvector is used to measure the centrality of its vertices. An example is Google's PageRank algorithm. The principal eigenvector of a modified adjacency matrix of the World Wide Web graph gives the page ranks as its components. This vector corresponds to the stationary distribution of the Markov chain represented by the row-normalized adjacency matrix; however, the adjacency matrix must first be modified to ensure a stationary distribution exists. The second smallest eigenvector can be used to partition the graph into clusters, via spectral clustering. Other methods are also available for clustering.

Calculation

책속에서 존재하는 Eigenvector와 Eigenvalue구하기의 난제는 다항식을 푸는 문제로 귀결된다. 하지만, 컴퓨터로 구현하고자 한다면 다항식을 푸는 문제 자체도 대단히 어려운 일이다. 해가 있는지 (허근인지 실근인지) 무엇보다도 소인수 분해와 같은 암호 해독과 같이 어려운 문제에 봉착하게 된다. 그래서 다항식 해법으로 접근하지 않고 Eigenvector와 Eigenvalue의 property(속성)을 이용하여 반복적인 연산을 통하여 실제 Eigenvector와 Eigenvalue에 수렴할 수 있는 근접한 값을 찾아 내는 방법을 사용한다. 여기에는 여러 가지 방법들이 존재한다.

Power iteration method
Shifted inverse iteration method
Rayleigh quotient method
Simultaneous iteration method
The QR method

이와 같은 반복적인 연산을 이용한 방식은 Eigenvalue와 Eigenvector가 존재한다는 가정 하에 다음과 같은 속성을 이용한다. 존재한다고 가정한 Eigenvalue들은 q_i 이고, Eigenvalue들은 λ_i 이다.

(|λ₁| > |λ₂| > … > |λ_n|)

그리고 추정하고자하는 Eigenvector는 실제 Eigenvector의 span으로 표현할 수 있다. 왜냐하면 Eigenvector는 해당 공간의 기저벡터(Basis vector)가 되기 때문이다. 그래서 다음과 같이 Eigenvector의 Linear combination으로 표현할 수 있다.

For the initial approximation v₀ , we choose a nonzero vector such that the linear combination

(만약 c₁ = 0 이라면, Power method는 수렴하지 않을 수도 있다. 그러면 다른 것을 초기추정치로 써야한다.)

이와 같은 추정치가 Eigenvector라고 한다면 실제 Eigenvector의 정의에 해당하는 조건식에도 부합되어야 한다.

그리고 A^kx = λ^kx의 확장된 속성으로부터

으로 전제할 수 있다. 여기서 주의 깊게 살펴보아야할 부분은 (λ_i / λ₁)^k의 부분이다. 분모에 해당하는 λ₁는 가장 큰 절대값을 갖는 Eigenvalue이기 때문에 k값이 커질수록 0의 값으로 수렴하게 된다.

그럼 나머지 항들은 사라지고 λ₁에 해당하는 (Dominant) Eigenvector의 값으로 v₀의 값은 수렴하게 된다. 기본적으로 이러한 개념하에 위의 반복적인 연산이 이루어진다.

그리고 이러한 기본 개념하에 Power iteration method와 Shifted inverse iteration method가 설명된다. 기타 다른 방식들도 이 방식에서 확장해 나아가는 형식을 취하고 있다.

Power iteration method

(http://en.wikipedia.org/wiki/Power_iteration)

Eigenvalues를 추정하기 위한 Power method는 반복적이다.

반복이 계속 진행될수록 x_k는 행렬 A와 계속 곱해지고, ||x_k|| = 1이 되도록 Normalize된다.

우선, 행렬A가 dominant eigenvector들에 해당하는 어떤 dominant eigenvalue를 가진다고 가정한다.

그리고나서 행렬A의 dominant eigenvector들 중 하나를 추정하는 초기추정벡터 x₀를 무작위로 선택한다.

이 초기추정벡터는 nonzero vector여야 한다.

최종적으로 다음과 같은 시퀀스를 만들 수 있다.

이 방식은 Eigenvalue 중 가장 큰 값에 해당하는 Dominant eigenvector를 구할 수 있다.

* Pseudo code of power iteration

Inverse iteration method

이 방식은 Eigenvalue 중 가장 작은 값에 해당하는 Eigenvector만 구할 수 있다. Power iteration 방식은 A의 Eigenvalue가 λ_i면 A^-1의 Eigenvalue가 1/λ_i가 되는 특성을 이용하여 A^-1에 Power iteration을 적용한다.

* Pseudo code of inverse iteration

Shifted inverse iteration method

A의 특정 Eigenvalue에 근접하는 값을 임의로 선택한 값이 u라고 하면 (A - u * I)의 Eigenvalue은 λ_i - u가 된다. 그리고 (A - u * I)에 inverse iteration을 적용하면 u값에 근접하는 Eigenvalue에 해당하는 Eigenvector를 구할 수 있다.

* Pseudo code of shifted inverse iteration (finding Eigenvector corresponding to Eigenvalue closed to u)

Rayleigh quotient iteration method

이 방식은 shifted inverse iteration에서 u값과 v값을 동시에 근사화시켜서 연산시간을 줄여주는 방식이다.

* Pseudo code of Rayleigh quotient iteration (finding Eigenvector corresponding to Eigenvalue closed to u)

Simultaneous iteration method

이 방식은 이전의 방식들이 한번에 하나의 eigenvector만을 구할 수 있지만 한 번에 모두 구할 수 있다.

* Pseudo code of simultaneous iteration

the columns of Q will converge towards a basis of Eigenvectors of A

The QR method

이 방식은 QR 분해를 반복적으로 수행하는 것이다. 이론이고 뭐고 Orthogonal column vector들은 항상 Q 행렬에 모이게 되고 Upper triangular 행렬은 R에 모이는 QR 분해를 Q 행렬에 반복적으로 recursive하게 적용하면 뭔가 유일한 Orthogonal columns vector가 나올 법하게 느껴진다.

* Pseudo code of the QR method

References

저작자표시 비영리 변경금지

SENS

Programming Note